Information
Learning Outcomes
After reading this section, you will be able to:
- Define the units for storing information on a modern computer
- Introduce the memory model for programming a modern computer
- Introduce the addressing system for accessing the memory of a modern computer
Introduction
The information stored in a computer includes program instructions and program data. This information is stored in bits in RAM. The instructions and data take the form of groups of bits. The two most common systems for interpreting information stored in RAM are the binary and hexadecimal numbering systems.
This chapter defines these numbering systems and their units and describes the memory model for addressing different groups of bits stored in the part of RAM associated with a program.
Fundamental Units
Bits
The most fundamental unit of a modern computer is the binary digit or bit. A bit is either on or off. One (1) represents on, while zero (0) represents off.
Since bits are too numerous to handle individually, modern computers transfer and handle information in larger units. As programmers, we define some of those units.
Bytes
The fundamental addressable unit of RAM is the byte. One byte consists of 2 nibbles. Each nibble consists of 4 bits.
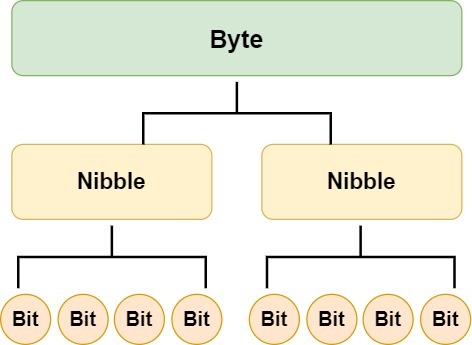
One byte can store any one of 256 (28) possible values in the form of a bit string:
| Bit Value | Decimal Value |
|---|---|
| 00000000 | |
| 00000001 | |
| 00000010 | |
| 00000011 | |
| 00000100 | |
| 00111000 | |
| 11111111 |
The bit strings are on the left. The equivalent decimal values are on the right. Note that our counting system starts from 0, not from 1.
Words
We call the natural size of the execution environment a word. A word consists of an integral number of bytes and is typically the size of the CPU's general registers. Word size may vary from CPU to CPU. On a 16-bit CPU, a word consists of 2 bytes. On a Pentium 4 CPU, the general registers contain 32 bits and a word consists of 4 bytes. On an Itanium 2 CPU, the general registers contain 64 bits, but a word still consists of 4 bytes.
Hexadecimal
The decimal system is not the most convenient numbering system for organizing information. The hexadecimal system (base 16) is much more convenient.
Two hexadecimal digits holds the information stored in one byte. Each digit holds 4 bits of information. The digit symbols in the hexadecimal number system are {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}. The characters A through F denote the values that correspond to the decimal values 10 through 15 respectively. We use the 0x prefix to identify a number as hexadecimal (rather than decimal - base 10).
| Bit Value | Hexadecimal Value | Decimal Value |
|---|---|---|
| 00000000 | ||
| 00000001 | ||
| 00000010 | ||
| 00000011 | ||
| 00000100 | ||
| 00111000 | ||
| 11111111 |
For example, the hexadecimal value 0x5C is equivalent to the 8-bit value 010111002, which is equivalent to the decimal value 92.
To learn how to convert between hexadecimal and binary refer to the chapter entitled Data Conversions in the Appendices.
Memory Model
The memory model for organizing information stored in RAM is linear. Any byte in memory is accessible through a map that treats each actual physical memory location as a position in a continuous sequence of locations aligned next to one another.
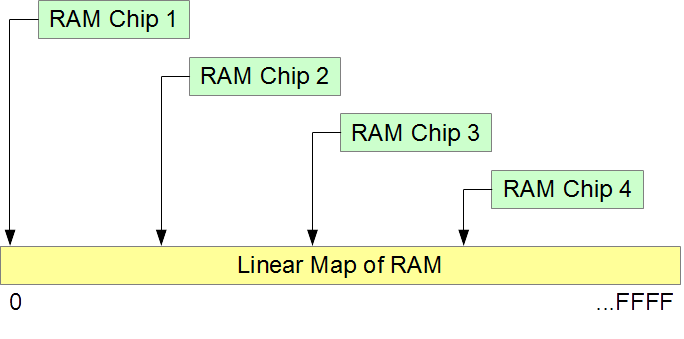
Addresses
Each byte of RAM has a unique address. Addressing starts at zero, is sequential, and ends at the address equal to the size of RAM less 1 unit.
For example, 4 Gigabytes of RAM
- consists of 32 (= 4 * 8) Gigabits
- starts at a low address of
0x00000000 - ends at a high address of
0xFFFFFFFF

Each byte, and not each bit, has its own address. We say that RAM is byte-addressable.
Sets of Bytes
The abbreviations for sets of bytes are:
- Kilo or k (=1024): 1 Kilobyte = 1024 bytes ~ 103 bytes
- Mega or M (=1024k): 1 Megabyte = 1024 * 1024 bytes ~ 106 bytes
- Giga or G (=1024M): 1 Gigabyte = 1024 * 1024 * 1024 bytes ~ 109 bytes
- Tera or T (=1024G): 1 Terabyte = 1024 * 1024 * 1024 * 1024 bytes ~ 1012 bytes
- Peta or P (=1024T): 1 Petabyte = 1024 * 1024 * 1024 * 1024 * 1024 bytes ~ 1015 bytes
- Exa or E (=1024P): 1 Exabyte = 1024 * 1024 * 1024 * 1024 * 1024 * 1024 bytes ~ 1018 bytes
The multiplying factor is 1024, not 1000. 1024 bytes is 210 bytes, which is approximately 103 bytes.
Limit on Addressability (Optional)
The maximum size of the memory that the CPU can access depends on the size of its address registers. The highest accessible address is the largest address that an address register can hold:
- 32-bit address registers can address up to 4 GB (Gigabytes) (addresses can range from 0 to 232-1, that is 0 to 4,294,967,295).
- 36-bit address registers can address up to 64 GB (Gigabytes) (addresses can range from 0 to 236-1, that is 0 to 68,719,476,735).
- 64-bit address registers can address up to 16 EB (Exabytes) (addresses can range from 0 to 264-1, that is 0 to 18,446,744,073,709,551,615).
Segmentation Faults
The information stored in RAM consists of information that serves different purposes. We expect to read and write data, but not to execute it. We expect to execute program instructions but not to write them. So, certain architectures assign the data read and write permissions, while assigning instructions read and execute permissions. Such permission system helps trap errors while a program is executing. An attempt to execute data or to overwrite an instruction reports an error. Clearly, the access has been to the wrong segment. We call such errors a segmentation faults.